Production Systems

• Recall the structure of an agent ...
  

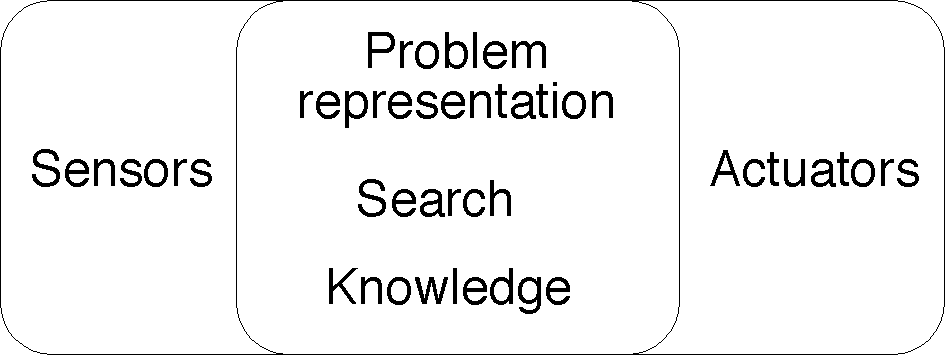
• A production system has 6 modules spread over the 3 parts of the central intelligence ...
  • Problem representation
    1. Dynamic problem and environment information in states, in a growing space of achieved states. Includes the initial state.
    • Other state lists and data structures as required.
  • Knowledge base
    2. Static information (which forms part of every state, and thus need not be duplicated).
    • Optionally: Semantic information for the static and dynamic information
  • Search control
    3. State transformation rules
    4. A strategy, with access to the problem representation and knowledge base (the three forms of information).
    5. A function that tests for a solution state
    6. The engine drives the system, and in conjunction with the control strategy and transformations forms the solution generator of a classical problem description.

• In general terms, the production system algorithm ...
  • Tests whether or not a solution state has been achieved
    • It may be necessary to generate several goal states before halting however, as a "best" solution may be required.
  • Selects achieved state+transformation pairs, based on the three forms of information.
  • Implements the selected transformations
  • Inserts the new states in the achieved space of states.
    • The achieved space of states has components:
      • The dynamic space is all known states
      • The frontier space is states from which transformations can still be done. Sometimes separated from the dynamic space.
      • The new space is states just discovered
    • Must produce motion through the state space.

• Influence of environment characteristics
  • Accessibility
    • Greater accessibility gives a greater possible role to knowledge
  • Dynamism
    • Knowledge changes during process - may be out of date
    • Semi-dynamic plays time off against performance.
  • Continuity
    • Data structures change
  • Agents
    • Multi-agent means a dynamic environment and/or a strategic problem

• Influence of problem characteristics
  • Determinism
    • Deterministic: Can choose transformation by predicting new states. Can plan ahead.
    • Searchable: Can search ahead.
    • Non-deterministic: Cannot predict new states. Cannot plan or search ahead. Requires repeated sensing.
  • Decomposability
    • If episodic, each episode can be treated separately. No relative state information between episodes.
  • Recoverability
    • Recoverable: Can do any number of transformations from any number of states. No need to plan ahead - good for non-deterministic problems.
    • Backtrackable: Must do one transformation from "current" state, but can always transform back. Needs a loop check for sure.
    • Non-recoverable: Must do one transformation from the current state.
  • Solution quality
    • Best solution possible if recoverable or backtrackable

• Production system engine algorithm, for
  • No environment
  • Deterministic, non-decomposable, recoverable, any solution problem
  • Choose state, expand all ways
  Suitable for, e.g., a theorem prover

  Problem = SenseProblem();
  KB = StaticPartOf(Problem);
  CurrentState = DynamicPartOf(Problem);
  NewStates = {CurrentState};
  DynamicStateSpace = {};
  FrontierStates = {};
  while (! SolutionFound(NewStates)) {
      FrontierStates += NewStates;
      StateToTransform = ExtractStateToTransform(FrontierStates,KB,DynamicStateSpace);
      NewStates = ApplyAllTransformations(StateToTransform);
      DynamicStateSpace += StateToTransform;
  } 

• To extend that to a best solution (e.g., a journey planner in a perfect world), call ...

  SolutionFound(NewStates,FrontierStates) 

  and install ...

  SolutionFound(NewStates,FrontierStates) {
  
      static BestSolutionSoFar = NULL;
  
      foreach (State in NewStates) {
          if (IsSolution(State) && State > BestSolutionSoFar) {
              BestSolutionSoFar = State;
          } 
      }
      foreach (State in NewStates + FrontierStates) {
          if (State could get better than BestSolutionSoFar) {
              return(FALSE);
          }
      }
      return(TRUE);
  } 

• Production system engine algorithm, for
  • No environment
  • Deterministic, non-decomposable, backtrackable, any solution problem
  • Can expand only one way
  Suitable for, e.g., simple maze solving.

  Problem = SenseProblem();
  KB = StaticPartOf(Problem);
  CurrentState = DynamicPartOf(Problem);
  DynamicStateSpace = {};
  while (! SolutionFound(CurrentState)) {
      Transformation = ChooseTransformationFromCurrentState(CurrentState,KB,DynamicStateSpace);
      if (Transformation == "backtrack") {
          CurrentState = PreviousState(CurrentState,DynamicStateSpace);
      } else {
          DynamicStateSpace += (CurrentState,Transformation);
          CurrentState = ApplyTransformation(CurrentState,Transformation);
      }
  } 

• Production system engine algorithm, for
  • Accessible, static, discrete, single agent environment
  • Non-deterministic, non-decomposable, non-recoverable, any solution problem
  • Can expand only one way

  Environment = SenseEnvironment();
  Problem = SenseProblem();
  KB = StaticPartOf(Problem) + Environment;
  CurrentState = DynamicPartOf(Problem);
  DynamicStateSpace = {};
  while (! SolutionFound(CurrentState)) {
      Transformation = ChooseTransformationFromCurrentState(CurrentState,KB,DynamicStateSpace);
      DynamicStateSpace += CurrentState;
      ApplyTransformation(CurrentState,Transformation);
      CurrentState = DynamicPartOf(SenseProblem());
  } 

• Production system engine algorithm, for
  • Accessible, dynamic, discrete, single agent environment
  • Deterministic, non-decomposable, recoverable, any solution problem
  • Choose state, expand one way
  Suitable for, e.g., web spider

  Problem = SenseProblem();
  KB = StaticPartOf(Problem);
  CurrentState = DynamicPartOf(Problem);
  DynamicStateSpace = {};
  while (! SolutionFound(CurrentState)) {
      DynamicStateSpace += CurrentState;
      Environment = SenseEnvironment();
      (FromState,Transformation) = ChooseStateAndTransformation(Environment,KB,DynamicStateSpace);
      CurrentState = ApplyTransformation(FromState,Transformation);
  } 

• Selecting applicable transformations
  • Matching
    • Involves search through the pre-conditions and finding all that match.
    • Slow if there are a lot of rules.
  • Indexing
    • Use the current state as an index into the rules to find appropriate rules.
    • Could use a partial index then search - the usual hashing techniques.
  • Matching with variables (unification)
    • Must keep bindings and apply them to the post-condition of the rule to get the new state.
    • More variables means more general rules but more matches with the problem state.
  • Approximate matching.
    • Arises from imprecise states and imprecise rules.

• Ability to add new information to the static knowledge base can change system behaviour. Can add new transformation rules that are consistent with old without disrupting the system.

• Production system characteristics
  • Monotonic production systems are those where an application of a rule from some state never prevents the application of another rule from that state later. This requires a recoverable problem.
  • A partially commutative prodution system allows commutation of the applications at the same state. This needs to be controlled when searching to prevent duplication of effort, e.g. ordering of transformation rules.
  • A commutative production system is both monotonic and partially commutative.

Exam Style Questions

• What are the components of a production system? Explain what each component does.
• Give the overall algorithm executed in a production system.
• Design a production system algorithm for ...
  • Partially accessible, static, discrete, single agent environment
  • Deterministic, non-decomposable, backtrackable, any solution problem