QC: Problem Set 1

Circuit computation model: classical and quantum

by: burt rosenberg
at: university of miami
date: aug 2022

Goals

The goals of this project are:

To open an account with the IBM Quantum Experience, and get familiarity with the quantum composer.
To introduce the circuit model of computation.
To introduce the quantum analogs of classical circuits: the qubit, and the quantum gate.
To discuss measurement for quantum outputs, and the Born Rule.
To introduce superposition and entanglement of qubits.

Classical Circuits

Programmers are given a certain model of a computer, called the RAM machine model. It is named after a major feature: the existence of a Random Access Memory, of data cells. Computation occurs in cycle of retrieving data from the cell, making a calculation, and returning the result to those or other data cells.

CLASSICAL BOOLEAN GATES
-----------------------

        +-----+
 x  --->+ NOT +---> ¬x       inverts the input, from 0 to 1, from 1 to 0
        +-----+
        
        +-----+
 x  --->+     |
        | AND +---> x ∧ y    is 1 only if both x and y is 1, else 0
 y  --->+     |
        +-----+
        
        +-----+
 x  --->+     |
        | OR  +---> x ∨ y    is 1 only if either x and y is 1, else 0
 y  --->+     |
        +-----+

        +-----+
 x  --->+     |
        | XOR +---> x ⊕ y    is 0 if x=y, else 1
 y  --->+     |
        +-----+

CIRCUIT COMPUTATION
-------------------

         +-----+                              TRUTH TABLE
   x ----+ NOT +----+--------------- ¬x        in   out       
         +-----+    |                          00 → 11
                    |   +-----+                10 → 01
                    +---+     |                01 → 00
                        | XOR +----- ¬x ⊕ y    11 → 10
   y -------------------+     |
                        +-----+
                        
PYTHON EQUIVALENT
-----------------

def circuit(x,y): return f"{int(not x != y)}{int(not x)}"
    
for x in range(2): 
    for y in range(2): print(f"{y}{x}->{circuit(x,y)}")

00->11
10->01
01->00
11->10

THE QUANTUM VERSION OF THE CLASSICAL CIRCUIT
--------------------------------------------

The X is the quantum version of NOT. The X with a "handle" is the 
controlled not, and is essentially and exclusive or of the 
control with the target, leaving the control unchanged and the 
target with the result of the exclusive or.

Another model is that a circuit of boolean gates. Each gate takes boolean input and calculates a boolean output. The gates are connected so the output of somegates become the inputs to other gates.

There are four classical gates, that are sufficient to build any boolean function, they are the not, the and the or and the exclusive or.

The not gate complements the input in calculating the output. The and and or perform their respective logical operation the two inputs, giving the result of the calculation as the output.

The exclusive or is a handy gate, that is true if the two inputs are unequal, and false if the two inputs are equal.

Here is an example circuit how gates are wired together. The first wire, x, has the value inverted; and the inverted value determines whether y will appear simply at the output or whether y will be inverted as well. The Truth Table is given, showing the output for all four possible inputs.

Also shown is a Python code, showing that the circuit model can be imbedded into a RAM model.

To some approximation, the RAM model of computation is the combination of a circuit model with a clocked storage area. The storage area presents its contents, or some small portion of its contents, to a circuit. The signals propagate until the output arrives, and the output is captured back into some portions of the storage area.

The circuit, rather than being fixed, as in this example, is configured for each computation cycle by an instruction, that is in turn fetched for another (or the same) storage area.

Quantum Circuits

The circuit model is used in the IBM quantum computers, with bits replaced by quantum bits, called qubits, and the gates replaced by quantum gates.

Superposition:
A classical bit is either 0 or 1. A qubit can be a linear combination of 0 and 1, called a superposition. The 0 is represented as the vector ∣0❭, the 1 as ∣1❭, so the mix is,
```
    φ = α∣0❭ + β∣1❭
```
where α and β are complex numbers subject to,
```
     α² + β² = 1.
```
Tensor Product:
A collection of classical bits, such as an 8 bit byte, consists of simply individual bits, brought together for convenience, or for data representation. Qubits tensor together, effectively creating a new data item for each combination of 0's and 1's.
The tensor operation is denoted by ⊗ use it as if it were the multiplication sign, however never commute the variables.
If qubit φ₁ is in state,
```
 
    φ₁ = α₁∣0❭ + β₁∣1❭
```
and qubit φ₂ is in state,
```
 
    φ₂ = α₂∣0❭ + β₂∣1❭
```
Then together there are four states,
```
 
    φ₁⊗φ₂  = (α₁∣0❭+β₁∣1❭) ⊗ (α₂∣0❭+β₂∣1❭) 
         = α₁α₂∣00❭ + α₁β₂∣01❭ + β₁α₂∣10❭ + β₁β₂∣11❭
```
Entanglement:
The tensor product demonstrated above does show that two qubits generate four storage slots. However, there remains an independence between the qubits. The resulting four coefficients can be explained by factoring into individual bits.
This is not necessarily the case. For instance, here is a possible state for two qubits,
```
    B =  (1/√2) (∣00❭ + ∣11❭)
```
This is called the Bell state, and it is not possible to create it as the tensor of two qubits. It is said to be entangled because while the first bit is in either 0 or 1, and the second bit is in either 0 and 1, they will agree on what state they are in, when a measurement is made on one, the other, or both.
Measurement: Borns Rule:
The classical bit is either 0 or 1. The measurement of a qubit must also result in 0 or 1, but it does so randomly, with probability guided by the weights of the superposition. Born's Rule states that the state φ,
```
    φ = α∣0❭ + β∣1❭
```
will be measured as 0 with probability ∣α∣², and as a 1 with probability ∣β∣². Note that these two probabilities add to 1.
Very little can be learned from a single measurement. If the measurement is 0, then it is learned that α is not exactly 0; if the measurement is 1, then it is learned tha β is not exactly 1. To learn more is frustrated by two important quantum facts,
1. Once a qubit is measured, old state is destroyed and its new state is that consistent with the measurement. I.e. if the measurement was 0, now the state of qubit is ∣0❭.
2. The no cloning theorm informs us that a qubit cannot be copied. You cannot run measurements on copies of the qubit, to determine α or β statistically.
In the case of our quantum circuits, the circuit can be run repeatedly, on equal inputs, and those outputs repeatedly measured to determine α or β. The run time for the algorithm will have to consider the number of repetitions needed. In this way, an algorithm with an exponential speed up because of superposition might not be overall faster because it will have to be repeated an exponential number of times to collect the output.
Max Born, for whom the rule is named, was a Noble Prize winning physicist and the grandfather of Olivia Newton-John.
Quantum Gates:
The quantum gates work on the superpositions as linear operators. The NOT, which is named X, works on the basis X∣0❭ → ∣1❭ and X∣1❭→ ∣0❭ Therefore, on a general state φ,
```
    X φ = X (α∣0❭ + β∣1❭)  =  Xα∣0❭ + Xβ∣1❭ =   αX∣0❭ + βX∣1❭ =  α∣1❭ + β∣0❭
```
Reversible::
Classical gates can calculate functions that cannot be inverted. For instance, if x∧y=0, we only know that x=y=1 is not possible.
Quantum circuits must be reversible, and in this means that no information is erased, and therefore no energy is consumed in the computation. A general way to make any operation invertible is to create a new qubit for the output, called the ancillary, imprint the calculated value onto the ancillary with an exclusive or operation. Assuming the ancillary is initialized zero, then the final result of the ancillary is the computed value. The inputs to the computation are all passed through directly.
For instance, an and of two inputs becomes are function from 3 qubits to 3 qubits, an ancillary qubit is used:
```
   ∧(x,y,w) ⟶ x, y, (x∧y)⊕w
```
Note that this can consume a lot of qubits, one for each operation; but cleverness and reuse can reduce the number of required ancillaries.

Exercise:

CREATING THE BELL STATE
-----------------------

TESTING ON CLASSICAL INPUTS
---------------------------

The controlled not gate works on two qubits, inverting the second qubit if and only if the first qubit is 1, else the seconnd qubit is unchanged,
```
      C|yx❭ ⟶ |(y⊕x)x❭
```
With x = x₀|0❭ + x₁|1❭, and y = y₀|0❭ + y₁|1❭, write out the output as,
```
     α₀₀ |00❭ +  α₁₀ |10❭ +  α₀₁ |01❭ +  α₁₁ |11❭
```
Factor this into a form,
```
   (b₀₀|0❭+b₁₀|1❭)a₀|0❭ + (b₀₁|0❭+b₁₁|1❭) a₁|1❭
```
and explain how this relates clearly to the c-not's operation.
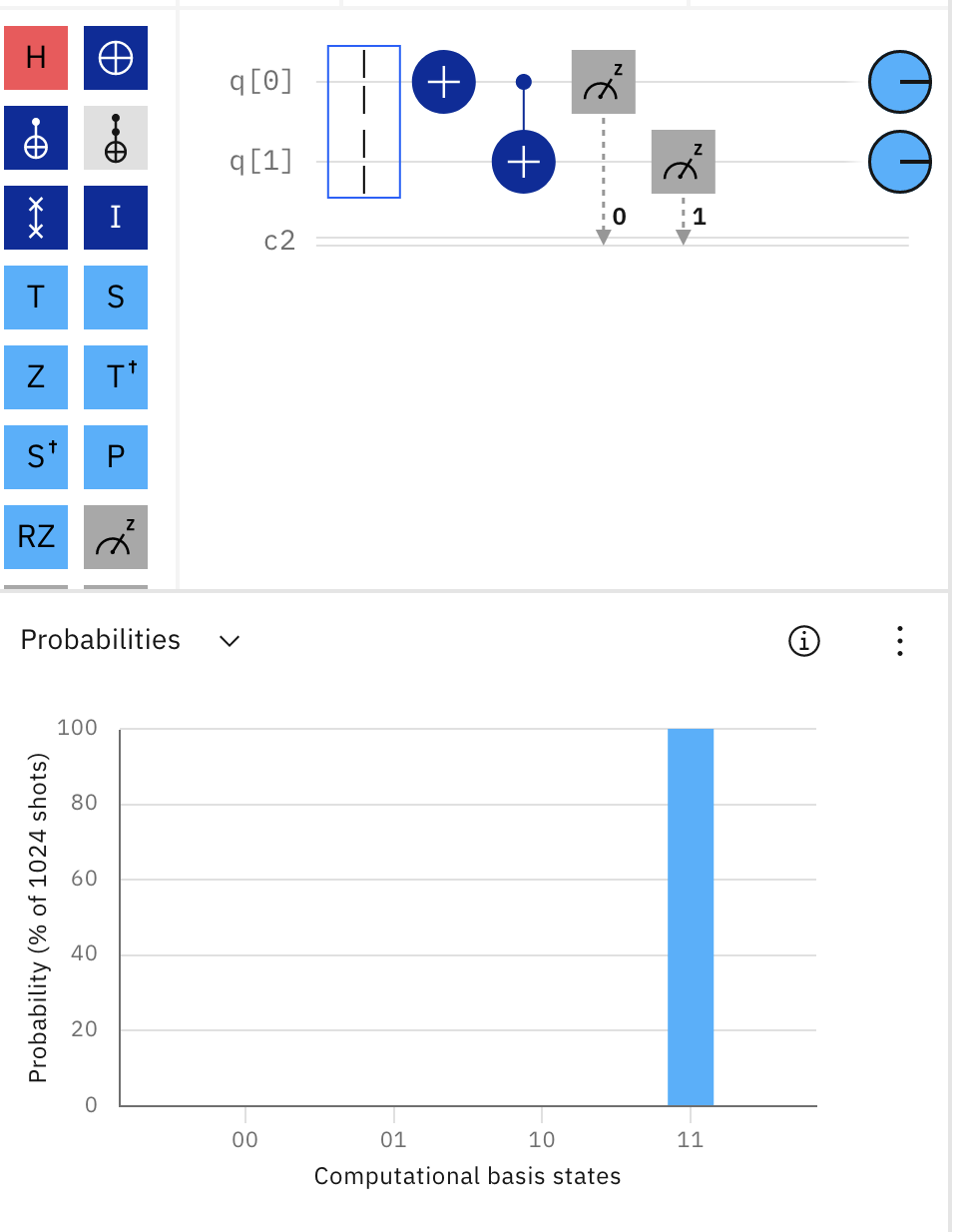
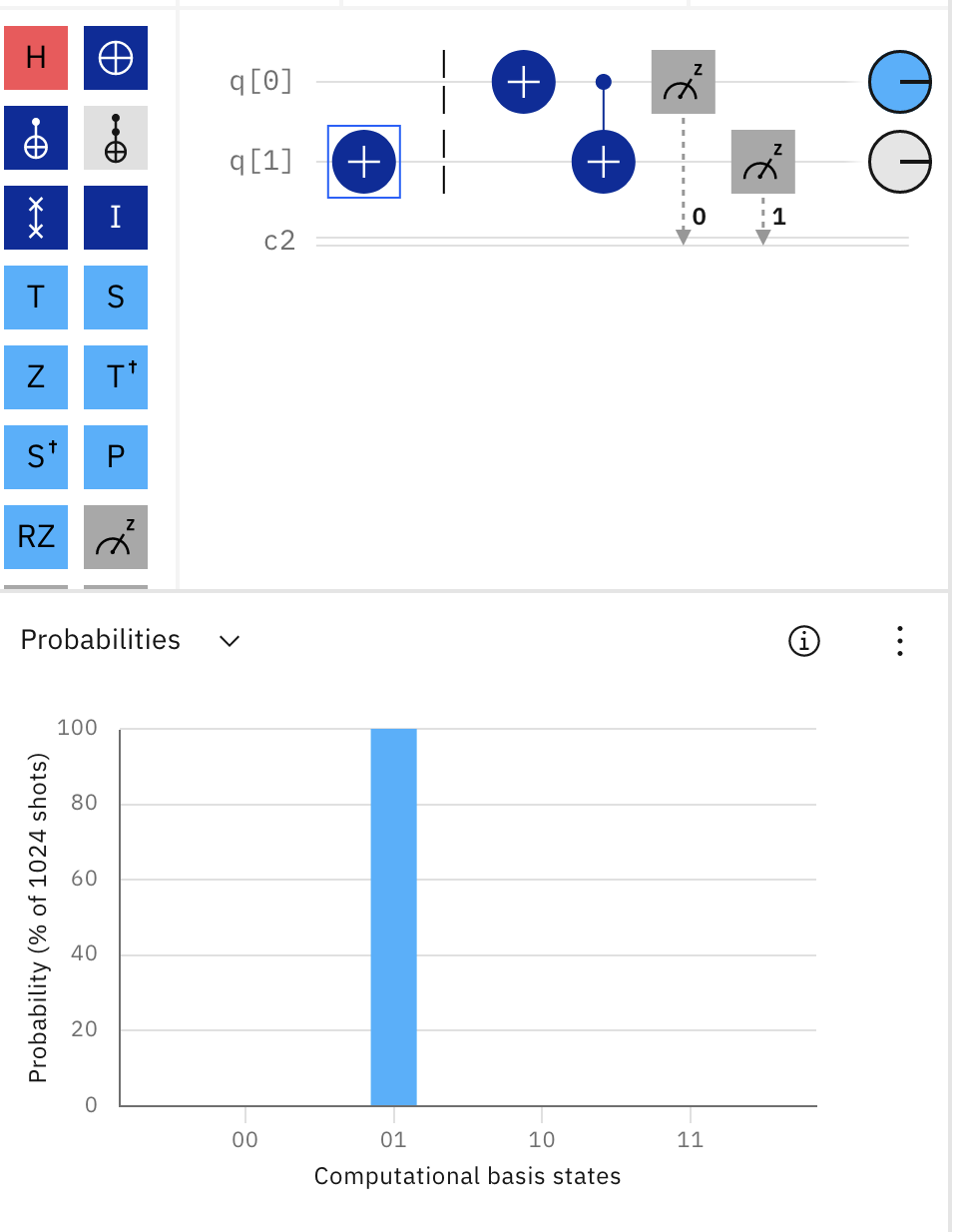
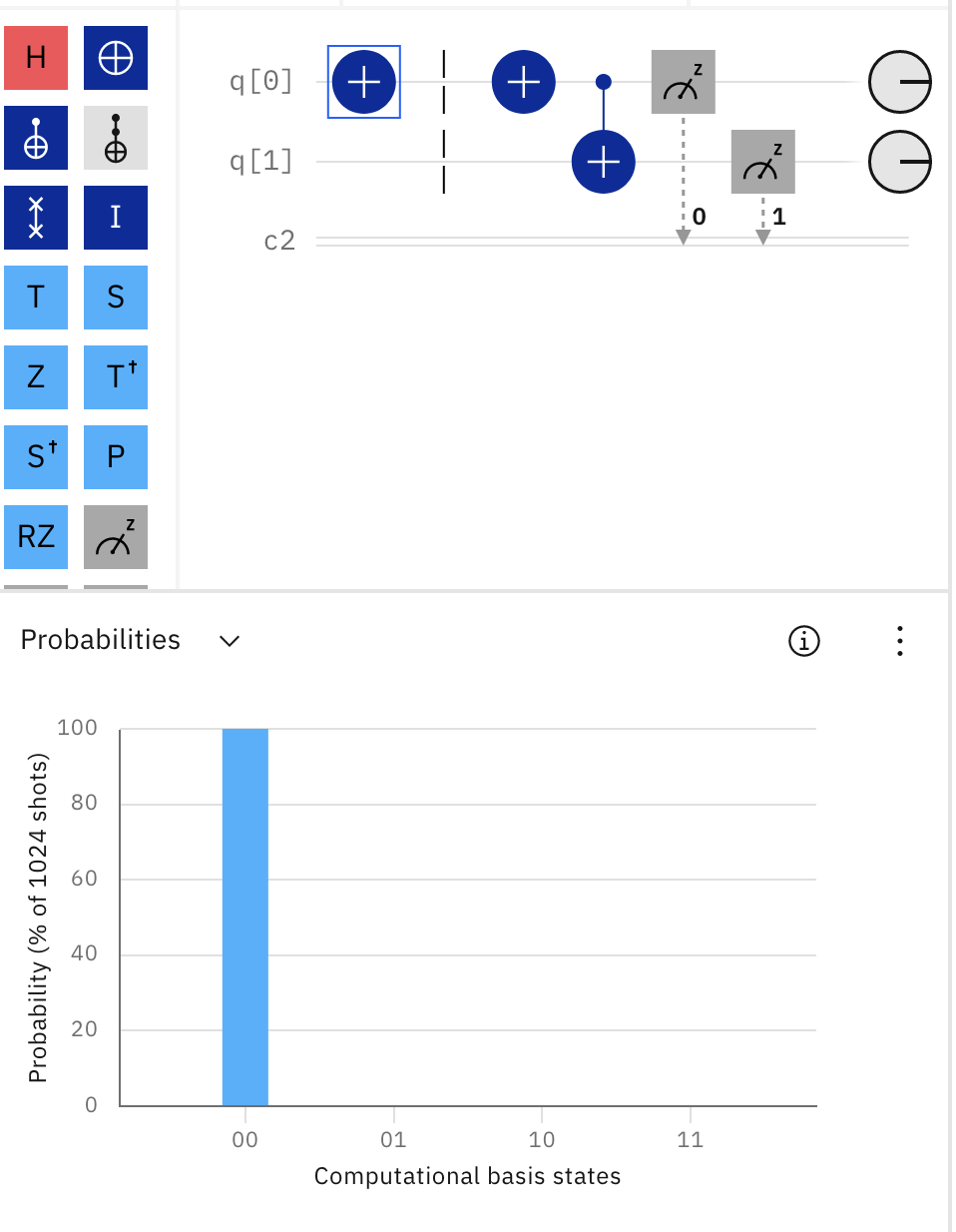
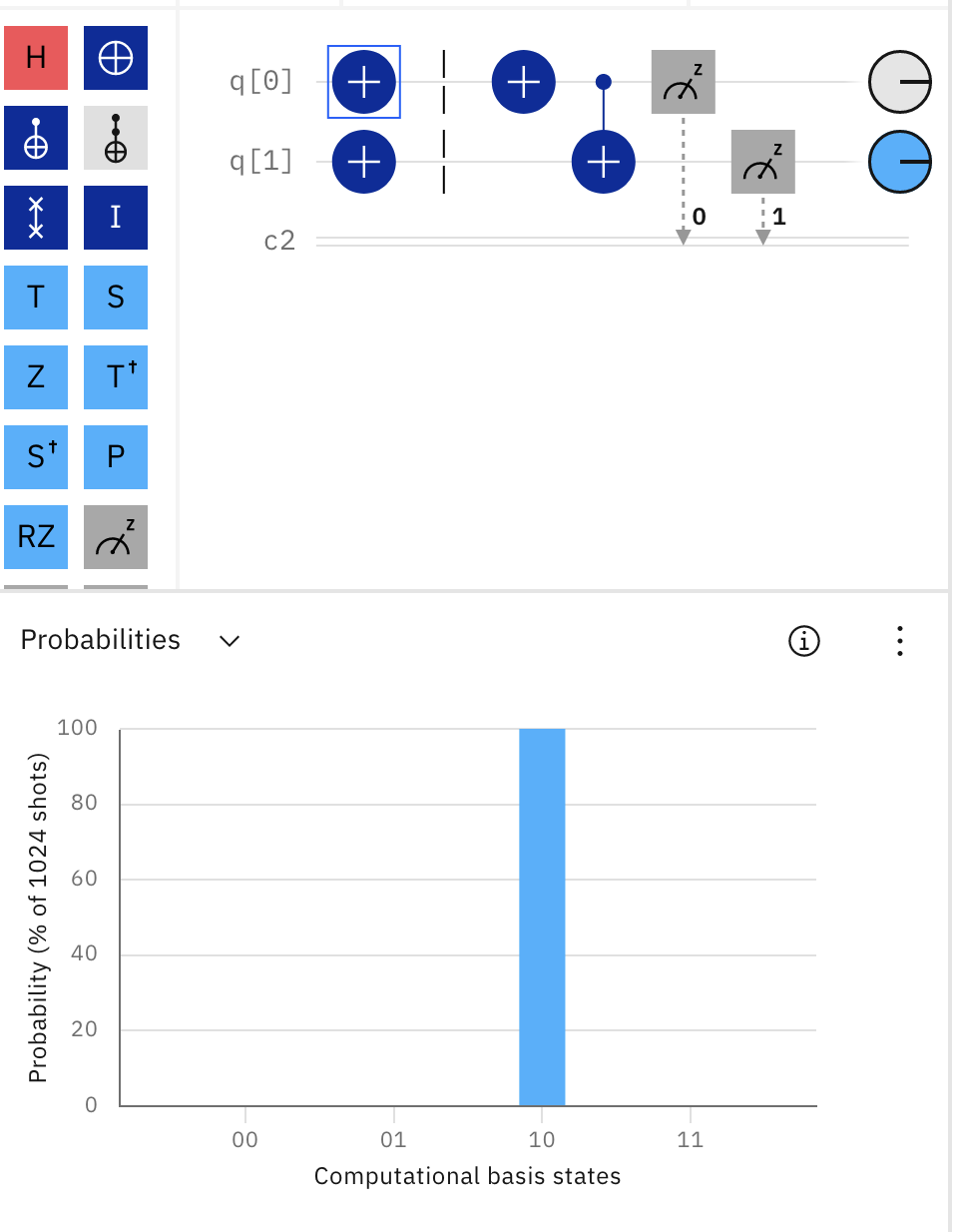
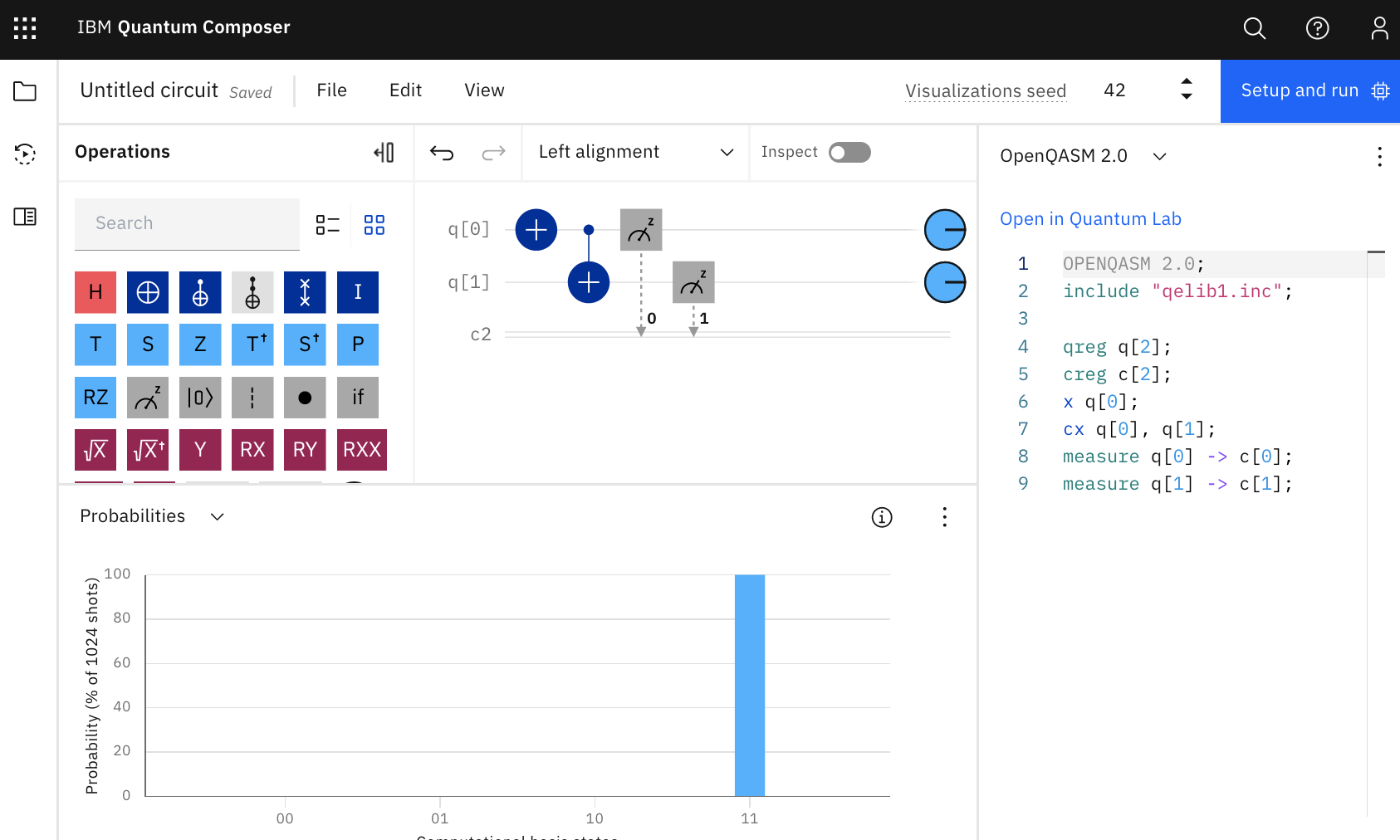
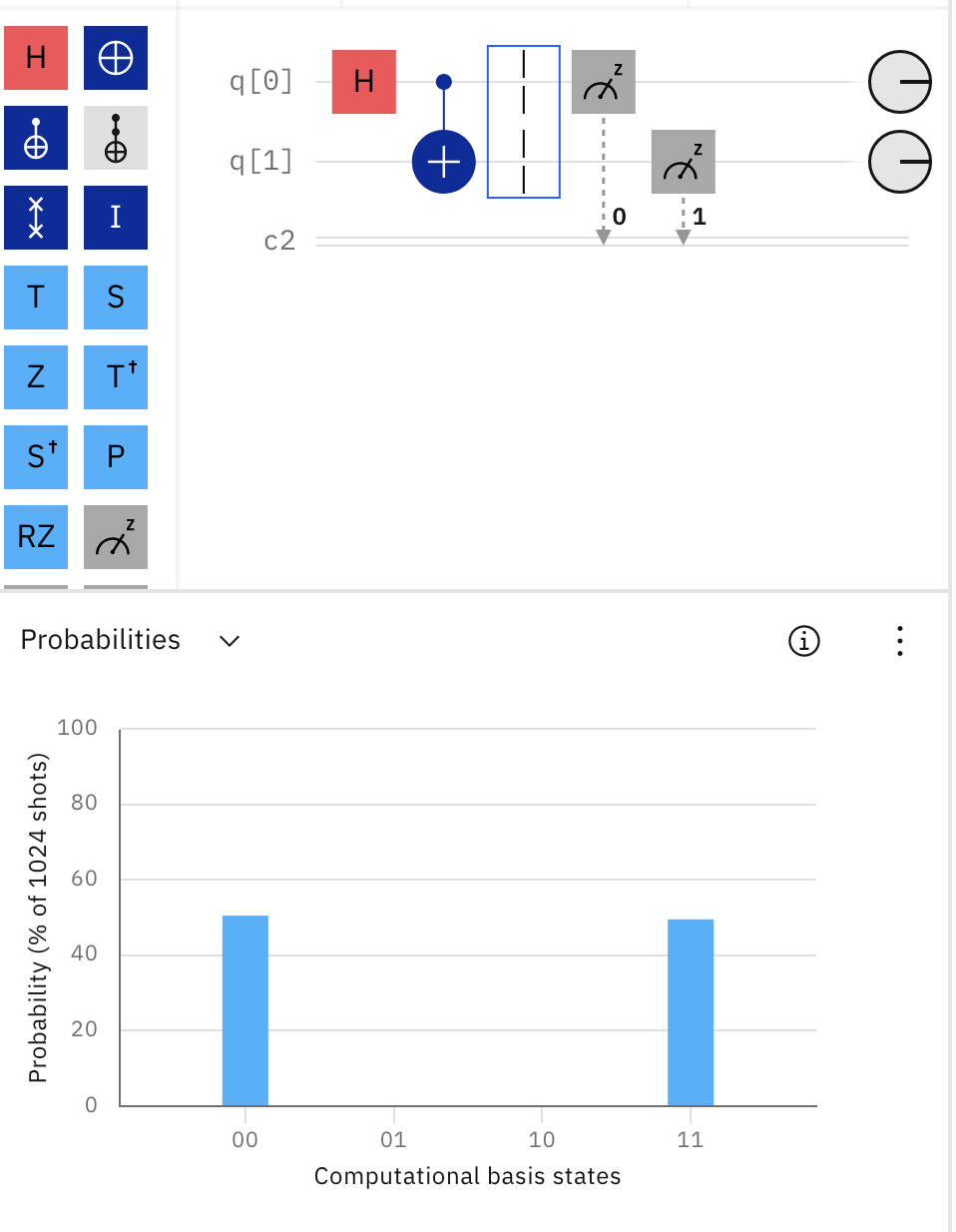
Test your results experimentally on simple 0, 1 inputs. The sequence of images from the quantum composer, titled: Testing On Classical Inputs, shows how this si done for a slightly different circuit.
The Hadamard gate takes a classical 0 or 1 to an equal superposition,
```
   H|0❭ = (1/√2)(|0❭+|1❭)
   H|1❭ = (1/√2)(|0❭-|1❭)
```
These resulting states are denoted |+❭ and |-❭, respectively.
Multiply out H(H(|0❭)) and verify that it equals |0❭; likewise for |1❭.
Show that HHφ for a general qubit value φ=α|0❭+βl|1❭, also gives φ. (I.e. that HH=identity).
Our circuit is modified to put a Hadamard gate before the c-not; this creates the Bell state,
```
   (1/√2)(|00❭+|11❭)
```
Explain; Show argue that this is a state impossible to achieve as a tensor of two independent qubits, as φ⊗φ'.
Discover a circuit that creates another Bell state,
```
   (1/√2)(|01❭+|10❭)
```
Do this on the quantum composer.
There are 4 other 2 qubit combinations such as (1/√2)(|01❭+|11❭). These are not entangled. For instance,
```
(1/√2)(|01❭+|11❭) = (1/√2)(|0❭+|1❭)|1❭ 
```
Discover the 4 circuits giving each of these states, and verify on the quantum composer.

Advanced Exercises:

CLASSICAL CIRCUIT FOR EXERCISE ?
--------------------------------

              +-----+
   x --+------+     |
       |      |     |
   y ----+----+ XOR +------------+
       | |    |     |            |
   z ------+--+     |            |
       | | |  +-----+            |
       | | |                     |  +-----+
       | | |  +-----+            +--+     |
       | | +--+     |    +-----+    | AND +-----
       | +----+ AND +----+ NOT +----+     |
       +------+     |    +-----+    +-----+
              +-----+

A popular riddle is how to swap the values between two register without using a third register. The solution to the riddle, classically, is the following sequence of exclusive or operations,

    x⊕y ⟶ y'
    y'⊕x ⟶ x'
    x'⊕y' ⟶ y''

Proof. The final value of x is,

   x' = y'⊕x = (x⊕y)⊕x = y

and the final value of y is,

   y''= x'⊕y' =  (y'⊕x) ⊕ (x⊕y) =y⊕y' = y⊕(x⊕y) = x

Create a quantum circuit that swaps two qubits. Build in the composer and test that it works on classical inputs. No ancillas are needed.

The Taffoli gate T works on three qubits,

   T|wyx❭ = (w⊕(y∧x)yx)

Considering w to be an ancilla, in computes the and of x and y.

What does the classical circuit pictured do? Create a quantum version; build in the composer and test on classical inputs (8 possible inputs from |000❭ through |111❭).

A bank of 3 Hadamards across three qubits creates an equal superposition of the eight classical states,

   H⊗H⊗H |000❭ = (1/√8)(|000❭+|001❭+|010❭+|011❭+|100❭+|101❭+|110❭+|111❭)

Run this superposition through the circuit, with the ancilla or ancillas qubits set to zero, and explain the output.

Design a classical circuit that outputs 1 if and only if exactly two of the three inputs is 1. Make a quantum version and test, as above.

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.

author: burton rosenberg
created: 22 aug 2022
update: 25 aug 2022